ADPCM算法

简介

ADPCM(Adaptive Differential Pulse Code Modulation, 自适应差分脉冲编码调制) 是一种音频信号数字化编码技术, 音频压缩标准 G.722, G.723, G.726 中都会使用到 ADPCM

预备知识

PCM-脉冲编码调制-Pulse Code Modulation

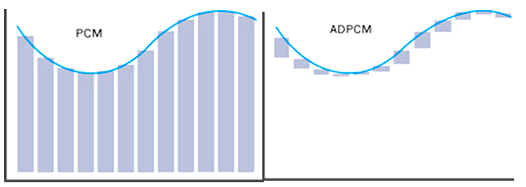
音频输入为 16bit 的有符号整数

假设输入样本分别为$s_{i}(1\leq i\leq 12)$

• 1024,1000,980,970,970,980,1000,1010,1024,1030,1020,1010

那么存储时需要开辟 12*16bit = 192bit，需要大量的空间
为了减少存储开销，Differential Pulse Code Modulation, 差分脉冲编码调制被提出

DPCM-差分脉冲编码调制-Differential Pulse Code Modulation

利用声波的连续性，一般来说，相邻采样值的差值较小，可以用较小的位数来存储
可将![[ADPCM算法#^c764ad]]进行差分运算$d_{i}=s_{i}-s_{i-1}(s_{0}=0)$，上述可编码为

• 1024,-24,-20,-10,0,10,20,10,14,6,-10,-10

若求原来的采样值$s_{i}$，只需$s_{i}=\Sigma{d_{i}}$（需要注意的是，DPCM 编码是无损的，也就是可以复原成原来的采样值）
大部分情况下，$d_{i}$只需要 4bit 来表示，但是存在一些情况，比如$s_{1}$无法用 4bit 的数值表示，于是 ADPCM 被提出

正课

ADPCM-自适应差分脉冲编码调制-Adaptive Differential Pulse Code Modulation

（本文以 IMA-ADPCM 算法实现进行说明）

主要思想

• 利用量化差分值(diffq)取代原有差分值(diff)进行差分运算

何为量化差分值？

量化差分值

由 DPCM 可以看出，差分值具有很大的范围，可以取遍$[-2^{15},2^{15}]$范围内的任何一个整数，无法用 4bit 的值来表示
而 ADPCM 的量化差分值是用 4bit 的 ADPCM 代码code与一个可变的步长step来表示，假定 step 可在$[0,2^{15}]$中取若干个数，构成一个 StepTable

现不加说明的给定 code(4bit)各位$\underline{a}\underline{b}\underline{c}\underline{d}$的含义

• a 代表符号，也就是正负
• b 是 1 时，代表 1 倍的 step 步长值
• c 是 1 时，代表 0.5 倍的 step 步长值
• d 是 1 时，代表 0.25 倍的 step 步长值

举个例子：

$code=(7)_{10}=(0111)_{2}$，代表 code 是正数，对应$1\times1+0.5\times1+0.25\times1=1.75倍$的步长值

$code=(5)_{10}=(1001)_{2}$，代表 code 是负数，对应$-(1\times0+0.5\times0+0.25\times1)=-0.25倍$的步长值

而量化差分值的计算方法是$diffq=code对应步长值的倍数\times当前的step步长值+1/8的步长值$

（注：1/8 的步长值是 IMA ADPCM 算法规定的，不同实现算法这部分不同）

这么计算之后，diffq 也可以取遍$[-2^{15},2^{15}]$的很大一部分数值，同时 diffq 只需要 4bit 的值与一个 step 值便可以计算出来，与 diff 的 16bit 相比，减小了很大的存储空间

现在回顾主要思想

利用量化差分值(diffq)取代原有差分值(diff)进行差分运算

既然要取代，我们就应该尽可能在当前的 step 下，尽可能的让 diffq 接近 diff 值
如何实现呢？

让 diffq 接近 diff

首先，diffq 应该要与 diff 有相同的符号，也就是说，$diff<0时，diffq<0$,那么 code 的第一位($a$)应该是 0，否则是 1

在当前 step 下，如果 diff 值大于一倍步长，那么为了让 diffq 尽可能靠近 diff，那么 diffq 值也应该大于一倍步长，根据 diffq 的计算方式，那么 code 的第二位($b$)应该是 1，否则 code 的第二位是 0

接下来将 diff 减去当前 step 值，如果这时候 diff 大于 0.5 倍步长，那么同理 code 的第三位($c$)应该是 1，否则是 0

接下来将 diff 减去 0.5 倍 step 值，如果这时候 diff 大于 0.25 倍步长，那么同理 code 的第四位($d$)应该是 1，否则是 0

这样，我们就得到了在当前 step 下最接近 diff 值的 diffq 的值，同时求出了 code 值

一个问题：

这样计算出来的 diffq 的绝对值的范围大致在 2 倍 step 范围内，假如此时的 diff 的绝对值远大于 step 值，要怎么办？

这就对每次选取的 step 值有着一定的要求

step 步长的选定

我们可以进行大胆的假定，假如这次的 diff 值远大于步长值，那么下一个采样值的 diff 值应该也是远大于这次的步长值，那么为了减小误差，我们就应该让下一次的步长值扩大 ^ce108a

我们定义一个 index 值，用于选取 step 值

其中 index 与 code 与 step 的关系应该满足：

• 当 index 变大的时候，step 对应变大；index 变小的时候，step 对应变小
• 当 code 大于 4 或者小于-4 的时候，也就是 diff 的绝对值大于 1 倍步长的时候，index 应该变大，这样可以使 step 变大

总结一下，index 受到 code 的影响，而 step 受到 index 的影响

我们观察 IMA-ADPCM 给定的 index 和 step 表(注意 IMA-ADPCM 中 index 是 8bit 整数)

/* Table of index changes */
const int IndexTable[16] = {
    0xff, 0xff, 0xff, 0xff, 2, 4, 6, 8,
    0xff, 0xff, 0xff, 0xff, 2, 4, 6, 8};
/* Quantizer step size lookup table */
const long StepTable[89] = {
    7, 8, 9, 10, 11, 12, 13, 14, 16, 17,
    19, 21, 23, 25, 28, 31, 34, 37, 41, 45,
    50, 55, 60, 66, 73, 80, 88, 97, 107, 118,
    130, 143, 157, 173, 190, 209, 230, 253, 279, 307,
    337, 371, 408, 449, 494, 544, 598, 658, 724, 796,
    876, 963, 1060, 1166, 1282, 1411, 1552, 1707, 1878, 2066,
    2272, 2499, 2749, 3024, 3327, 3660, 4026, 4428, 4871, 5358,
    5894, 6484, 7132, 7845, 8630, 9493, 10442, 11487, 12635, 13899,
    15289, 16818, 18500, 20350, 22385, 24623, 27086, 29794, 32767};

step 表随着下标的增加而增加
index 表在 code 为 0~3 与-3~0 的时候为 0xff，其余为 2，4，6，8

我们令

index = index + IndexTable[code]

step = StepTable[index]

code 为 0~3 与-3~0 时，$index=index+0xff$,由于 index 是 8bit 数据，必然会溢出，溢出之后得到的数据相当于 index-1，此时对应的 step 值变小

code 大于 4 或者小于-4 时，index 加上了一个大于 0 的数，使 index 变大，此时对应的 step 值变大，符合要求

注意，这些 step 与 index 是在当前采样值下计算的，是在下一次的采样值下使用的

现在 step 也解决了，也编码完了，如何解码呢

解码

同 DPCM 原理一样，通过计算量化差分值的和，得到解码数据
不过，此时得到的数据与原数据是有差异的，故而 ADPCM 是有损压缩

代码实现

#include <cstdio>
#include <iostream>
using namespace std;
/* Table of index changes */
const int IndexTable[16] = {
    0xff, 0xff, 0xff, 0xff, 2, 4, 6, 8,
    0xff, 0xff, 0xff, 0xff, 2, 4, 6, 8};
/* Quantizer step size lookup table */
const long StepSizeTable[89] = {
    7, 8, 9, 10, 11, 12, 13, 14, 16, 17,
    19, 21, 23, 25, 28, 31, 34, 37, 41, 45,
    50, 55, 60, 66, 73, 80, 88, 97, 107, 118,
    130, 143, 157, 173, 190, 209, 230, 253, 279, 307,
    337, 371, 408, 449, 494, 544, 598, 658, 724, 796,
    876, 963, 1060, 1166, 1282, 1411, 1552, 1707, 1878, 2066,
    2272, 2499, 2749, 3024, 3327, 3660, 4026, 4428, 4871, 5358,
    5894, 6484, 7132, 7845, 8630, 9493, 10442, 11487, 12635, 13899,
    15289, 16818, 18500, 20350, 22385, 24623, 27086, 29794, 32767};

struct ADPCM_Data
{
    int index;
    int sample;
};

ADPCM_Data prevSample = {0, 0}; // 前一个数据，初始均为0，0，通过前一个数据计算的index值与采样值，来计算当前采样值的step值

/*
code代表着量化差分值是几倍的步长，
0000-1111
4位
从左到右，第一位是符号位，代表量化差分值的正负
第二位是数值位，代表量化差分值的绝对值是步长的1倍或者0倍
第三位是数值位，代表量化差分值的绝对值是1/2步长的1倍或者0倍
第四位是数值位，代表量化差分值的绝对值是1/4步长的1倍或者0倍
量化差分值默认有step的1/8（具体原因我也不知道...也许是1/4step的0与1的统计平均值，所以取1/8step）
也就是diffq（也就是量化差分值）只能是step的+-(0,0.25,0.5,0.75,1,1.25,1.5,1.75)+0.125的倍数
*/

/*
diff差分值与diffq量化差分值的关系
diffq在精度允许情况下，可以看作diff（压缩损失由来）
diffq只能是step的某个倍数，而diff则可以随意取
diffq则是在step的倍数中的一个尽可能接近diff的一个数
*/

/*
若code大于4或者小于-4时，说明差分值大于1倍的步长，我们可以预测下一次的差分也是大概率大于1倍步长，
因此我们应该变大步长值，在index = IndexTable[code]可以看出
1. code在0-3（对应差分值是步长的1/8倍到1.125倍之间）或者8-11（对应差分值是步长的-1/8倍到-1.125倍之间）时，
也就是这时候差分值的绝对值是小于等于一倍的步长时，也就是说步长可能大了一点点，
IndexTable为0xff，index（8位无符号数）加上0xff，必然导致溢出，
由二进制的知识可以知道，溢出后得到的值实际上就是index-1,这样使步长略微减小，保持在1倍附近
2. code在4-7（对应差分值是步长的1.125倍到1.875倍之间时）或者12-15（对应差分值是步长的-1.125倍到-1.875倍之间时）
也就是这时候差分值的绝对值大于一倍步长的时候，也就是说步长可能小了一点点
IndexTable是2，4，6，8，这样使index变大，使得下一次的step值扩大
这样使下一次的差分值保持在1倍附近
这应该就是IndexTable与StepSizeTable构造原理
*/

int ADPCM_Encoder(int sample)
{
    int code = 0;
   
    int predSample = prevSample.sample; // 获取之前的采样数据，16bit
    int index = prevSample.index;       // 获取之前的index值，8bit无符号整数

    int step = StepSizeTable[index]; // 获取步长

    int diff = sample - prevSample.sample; // 获取当前样本值和上一个样本值的差分数值

    if (diff > 0) // 差分大于0，则code符号位不需要改变
        code = 0;
    else // 差分值小于0，code修改符号位，也就是和2进制的(100)进行或运算，也就是和10进制的(8)进行或运算
    {
        code |= 8;    // 改变符号位
        diff = -diff; // diff变成正的
    }

    int tempstep = step;

    if (diff >= tempstep) // diff大于1倍步长的话
    {
        diff -= tempstep; // 减去步长，获取剩余的差分值
        code |= 4;        // 修改第二位为1
    }
    tempstep >>= 1; // 步长变为原来的一半

    if (diff >= tempstep) // diff仍大于0.5倍步长的话
    {
        diff -= tempstep; // 减去步长，获取剩余的差分值
        code |= 2;        // 修改第二位为1
    }
    tempstep >>= 1; // 步长变为原来的一半

    if (diff >= tempstep) // diff仍大于0.25倍步长的话
    {
        diff -= tempstep; // 减去步长，获取剩余的差分值
        code |= 1;        // 修改第一位为1
    }

    int diffq = step >> 3; // 量化差分值，默认有1/8的步长
    if (code & 4)          // 如果差分值大于步长的一倍，量化差分值加上步长的1倍
    {
        diffq += step;
    }
   
    step >>= 1;   // 步长变为原来的一半
   
    if (code & 2) // 如果差分值大于步长的0.5倍，量化差分值加上步长的0.5倍
    {
        diffq += step;
    }
    step >>= 1;   // 步长变为原来的一半
    if (code & 1) // 如果差分值大于步长的0.25倍，量化差分值加上步长的0.25倍
    {
        diffq += step;
    }

    if (code & 8) // 符号位是1，说明量化差分值是负的，预测值也就减去diffq
        predSample -= diffq;
    else // 符号位是0，说明量化差分值是正的，预测值也就加上diffq
        predSample += diffq;

    // 处理数据溢出
    if (predSample > 32767)
        predSample = 32767;
    else if (predSample < -32767)
        predSample = -32767;

    index += IndexTable[code];
    if (index < 0)
        index = 0;
    index &= 0xff; // 舍弃高位溢出，本质是因为我定义了index是32位整数，手动&0xff，舍弃高位数字
    if (index > 88)
        index = 88;

    // 此为数据已经decode完毕，更新prevSample
    prevSample.sample = predSample;
    prevSample.index = index;

    return (code & 0x0f);
}

int ADPCM_Decoder(int code)
{
    int predSample = prevSample.sample; // 获取之前的采样值
    int index = prevSample.index;       // 获取之前的index值

    int step = StepSizeTable[index]; // 获取步长

    int diffq = step >> 3; // 量化差分值带有默认的1/8步长
    if (code & 4)          // 如果code的二进制的第二位是1，也就是code&4是1，说明量化差分值是大于一倍步长
        diffq += step;     // 加上步长
    step >>= 1;            // 步长减半
    if (code & 2)          // 如果code的二进制的第三位是1，也就是code&2是1，说明量化差分值是大于0.5倍步长
        diffq += step;     // 加上步长
    step >>= 1;            // 步长减半
    if (code & 1)          // 如果code的二进制的第四位是1，也就是code&1是1，说明量化差分值是大于0.25倍步长
        diffq += step;     // 加上步长

    if (code & 8)            // 如果符号位是1，说明量化差分值是负数
        predSample -= diffq; // 减去量化差分值
    else                     // 否则
        predSample += diffq; // 加上量化差分值
   
    // 处理数据溢出
    if (predSample > 32767)
        predSample = 32767;
    else if (predSample < -32767)
        predSample = -32767;

    index += IndexTable[code];

    if (index < 0)
        index = 0;
    index &= 0xff;
    if (index > 88)
        index = 88;

    // 此为数据已经encode完毕，更新prevSample
    prevSample.sample = predSample;
    prevSample.index = index;

    return predSample;
}

int main()
{
    int sample[16] = {0x0010,
                      0x0020,
                      0x0030,
                      0x0040,
                      0x0050,
                      0x0050,
                      0x0050,
                      0x0040,
                      0x0400,
                      0x0400,
                      0x0400,
                      0x0400,
                      0x0400,
                      0x0400,
                      0x0400,
                      0x0400};
    int EncodeSample[16];
    for (int i = 0; i < 16; i++)
    {
        EncodeSample[i] = ADPCM_Encoder(sample[i]);
        printf(", code:%d\n", EncodeSample[i]);
    }
    prevSample = {0, 0};
    int DecodeSample[16];
    for (int i = 0; i < 16; i++)
    {
        DecodeSample[i] = ADPCM_Decoder(EncodeSample[i]);
        printf("%x ", DecodeSample[i]);
    }
}